♦ Décrit les variations d'abondance dans l'espace et dans le temps des diverses espèces et en recherche les causes. Elle tente de comprendre les facteurs responsables des variations d'effectifs au sein d'une population. Ce terme diffère de celui de cinétique qui est l'étude descriptive des effectifs, de la densité et de la structure des populations et leurs transformations au cours du temps.
- Étude des fluctuations en nombre des populations d’animaux ou de plantes, autrement dit, c’est une discipline qui s’intéresse particulièrement aux variations d’abondance des populations et leurs compositions.
- La dynamique des populations appelée démoécologie forme avec la génétique des populations la discipline appelée la Biologie des populations.
- Les autres branches de cette science globale (l’écologie) sont : l’Autoécologie encore appelée écophysiologie s’intéresse à l’étude de l’action des
- facteurs écologiques sur les végétaux et les animaux pris isolément ;
- la biocoenotique a pour objet d’étude les communautés ;
- la synécologie s’intéresse à l’étude des niveaux d’organisation du vivant les plus complexes que sont l’écosystème et la biosphère tout entière.
- La matière objet d’étude de la dynamique des populations est la population. Elle est définie comme un ensemble d’individus de même espèce ayant la possibilité de s’apparier parce qu’ils occupent un même milieu. Parmi tous les individus interféconds qui composent une espèce donnée, constituent une population, les individus de cette espèce concrétisent leur interfécondité par des croisements réguliers. Dans la nature, l’espèce est organisée en populations. Les individus d’une même population utilisent les mêmes ressources et sont exposés aux mêmes contraintes du milieu et de ce fait ont une même fonction dans l’écosystème auquel ils appartiennent.
- L’entité biologique constituée par un ensemble de populations d’espèces vivant à un moment donné, dans un endroit déterminé, dans des conditions d’un milieu déterminé et qui présentent une organisation spatiale et temporelle ainsi que des interactions fonctionnelles structurantes est appelée une communauté.
- La communauté de l’ensemble des êtres vivants inféodés à un biotope considéré est appelée la biocénose qui comprend la phytocénose formée par les êtres vivants végétaux et la zoocénose constituée par l’ensemble des animaux de l’écosystème.
- Le niveau le plus complexe de l’organisation biologique étudié par l’écologie est la biosphère. Ce terme désigne la partie de la planète terre où la vie est possible en permanence et qui renferme l’ensemble des êtres vivants.
- La biosphère comprend trois compartiments :
- la lithosphère qui est la partie limitée aux couches superficielles de l’écorce terrestre ;
- l’hydrosphère ou l’océan mondial, c'est-à-dire le milieu liquide représentant les sept dixièmes de la surface planétaire ;
- l’atmosphère qui est l’enveloppe externe constituée par la couche gazeuse homogène formant la partie périphérique de la Terre.
- Une population en contact avec d’autres populations de même espèce par les phénomènes de migrations (cas des animaux), de dispersion de semences et de pollen (cas des plantes), est dite une population ouverte.
- Un ensemble de populations ouvertes interconnectées forme une métapopulation.
- Une population isolée n’ayant pas de contact avec une autre de la même espèce pour occasionner d’éventuels croisements pour la reproduction est appelée une population fermée.
- Du fait qu’elle est isolée et n’échange plus ses gènes avec les autres populations de la même espèce, une population fermée peut évoluer au cours des temps géologiques et se différencier progressivement de l’espèce initiale. Le processus de formation des espèces (appelée spéciation) qui résulte de l’isolement géographique des populations est appelé la spéciation allopatrique.
- Le processus de formation d’espèces qui se déroule à l’intérieur d’une même aire géographique est appelé la spéciation sympatrique.
> La croissance d'une population est caractérisée par une série d'équations :
N(t + Δt) = N(t) + B + I - E - D - H
où N(t) : Nombre d'individus de l'année t
N(t + Δt) : Nombre d'individus après une ou plusieurs
saisons de reproduction
B (birth) : Nombre d'individus nés dans cette population
I (immigration) : Nombre d'individus entrant dans cette population
E (emigration) : Nombre d'individus sortant de cette population
D (death) : Nombre d'individus morts dans une population
H (human exploitation) : Nombre d'individus exploités
- La population est croissante quand : B+I > H+D+E.
- La population est décroissante quand : B+I < H+D+E.
> Les éléments intervenant sur ces différents compartiments sont :
Les facteurs endogènes interviennent également mais, contrairement aux précédents, ils ne peuvent faire l'objet d'interventions. On y classe le taux de fécondité, la longévité, les comportements sexuels... En termes d'applications pratiques, comprendre la dynamique d'une population animale permet de gérer au mieux son exploitation éventuelle, ceci afin de ne prélever que le surplus et de laisser la population de reproducteurs à un niveau stable.
> L'importance de la dynamique des populations, élément de base de la compréhension de la croissance de la population humaine et de manière générale, des tendances des espèces, a conduit à l'élaboration de modèles de plus en plus complexes.
1. Le premier est le modèle de croissance exponentielle, ou malthusienne. Il repose sur le concept qu'une population croît proportionnellement à son effectif de telle sorte que :
dN / dt = nN - mN = (n-m) N = rN
où r : Taux d'accroissement intrinsèque (dit paramètre malthuséen),
avec m (mortalité) = M / N et n (natalité) = N / M
de telle sorte que r = n-m.
Le modèle exponentiel de Malthus repose sur plusieurs hypothèses :
- Une reproduction continue avec des taux de naissance et de mortalité constants (pas de saisonnalité dans la reproduction) et une absence de migration
- Une identité des organismes (pas de structure d'âge marquée)
- Un environnement spatial et temporel constant (ressources non limitées, taux d'accroissement indépendant de l'effectif de la population).
Ce modèle aboutirait à une surpopulation d'une espèce dans la mesure où le taux d'accroissement est indépendant de l'effectif, ce qui est crédible sur le plan mathématique mais ne l'est pas sur le plan biologique.
2. Le modèle logistique
Il a été développé par le mathématicien belge Pierre Verhulst (1838) qui a suggéré que le taux d'accroissement de la population peut être limité par sa propre densité (notion de densité-dépendance) ou par la quantité de ressources disponibles dans le milieu. Ainsi, en supposant que la population étudiée soit dans un système fermé, ses effectifs vont augmenter en fonction de la population initiale, mais cette augmentation va être limitée par le milieu et les ressources qui vont contribuer à décroître les naissances et à augmenter la mortalité.
L'équation relative à l'augmentation de la population au cours du temps va donc prendre la forme :
dN / dt = rN (1 - N/K)
où K : Capacité limite du milieu ;
quand N=k ou N=0, l'équation est à l'équilibre : dN/dt=0
r : Taux de croissance intrinsèque défini plus haut
Le paramètre K est généralement interprété comme le nombre d'organismes pouvant être nourris ou abrités par les ressources. Il a une signification biologique pour les populations avec une forte interaction entre les individus contrôlant leur reproduction.
No < K : population augmente et atteint un plateau. Il s'agit de la courbe logistique
No > K : diminution des populations jusqu'à un plateau
No = K ou N = 0 : l'équation est à l'équilibre, la population ne change pas
Lors d'une croissance logistique, la taille de la population tend vers la capacité de charge K. Tant que la taille de la population de dépasse pas K, la population continue de croître. Quand N excède K, la population décroît. K est la situation d'équilibre d'une population sous l'effet d'une croissance logistique.
Ce modèle ne peut être utilisé qu'en fonction de certaines conditions :
- Ressources limitées
- Identité des individus composant la population
- Pas de migration
- Constance des paramètres r et K
- Pas d'effet stochastique (qui relève du hasard).
3. Modèle de Lotka-Volterra ou modèle proie-prédateur
Ce modèle a été proposé indépendamment par Alfred Lotka en 1925 et Vito Volterra en 1926 et est fondé sur deux principes :
- En absence de proies, les prédateurs disparaîtraient ; dy/dt = - my
- En absence de prédateurs, les proies se multiplieraient : dx/dt = rx
La prédation est proportionnelle au produit des proies et des prédateurs lors de rencontres aléatoires (axy) :
dx / dt = rx - axy
dy/dt = - my + e axy
où a : Efficacité de prédation
e : Efficacité de conversion de nourriture en reproduction
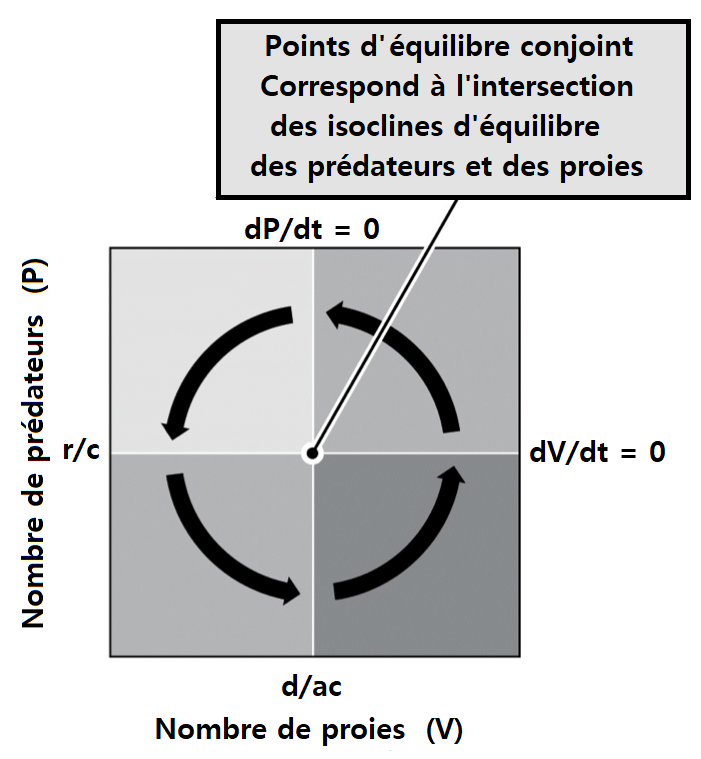
> Dans les équations du modèle de Lotka-Volterra, la vitesse maximale d’accroissement d’une population de prédateurs se situe au moment de la densité maximale de ses proies reflétant le fait que le taux de multiplication du prédateur dépend essentiellement de la disponibilité de sa ressource almentaire. Réciproquement, la vitesse maximale de décroissance d’une population de proies se situe au moment de la densité maximale de prédateurs reflétant le fait que la cause de mortalité est la prédation. Les oscillations des deux populations sont donc de même fréquence mais décalées d’un quart de période.
Le modèle de Lotka et Volterra est fondé des hypothèses qui, selon différents auteurs, ne reflètent pas la réalité biologique :
- il n'intègre pas la capacité limite du milieu pour la proie dont la croissance n'est pas supposée dépendre de la quantité de nourriture disponible ;
- il suppose que le prédateur est strictement monophage et ne dispose pas de proies de substitution ;
- il admet que le taux de prédation est constant, indépendamment de la densité et de la structure démographique de la population-proie ;
- il ignore l'existence de temps de latence qui tendent à rendre instables les interactions proieprédateur. En effet, ces temps de latence peuvent amplifier les oscillations et même conduire à l'extinction d'une des deux populations.
♦ Équivalent étranger : Population dynamics.



