♦ Graphe (constitué de noeuds et d'arcs), associé à un ensemble de tables de probabilités de noeuds (TPN), ainsi nommées car il y en a une et une seule par noeud du graphe. Les noeuds représentent des variables aléatoires discrètes. Les arcs représentent des relations de cause à effet entre variables. Le graphe est acyclique et ne contient pas de boucle. Les arcs représentent des relations entre variables qui sont soit déterministes, soit probabilistes. Ainsi, l'observation d'une ou plusieurs causes n'entraîne pas systématiquement l'effet ou les effets qui en dépendent, mais modifie seulement la probabilité de les observer. Le graphe est aussi appelé la "structure" du modèle, et les tables de probabilités ses paramètres.
Généralement, la structure est définie par des experts et les tables de probabilités calculées à partir de données expérimentales. Les réseaux bayésiens permettent d'analyser des quantités de données utiles à la prise de décision, au contrôle ou à la prévision. Ils conjuguent les avantages de diverses approches :

• La compréhensibilité des modèles symboliques
• Les fondements probabilistes rigoureux des méthodes statistiques
• La structure en réseau de composants simples des approches connexionistes

Les réseaux bayésiens représentent toutes les relations entre les attributs (décrivant les exemples) et ils permettent une utilisation multidirectionnelle.

> Le réseau bayésien peut être directement construit ou être pris d’une base de données. Tout mélange des deux approches est également possible. Une fois construit, le réseau peut produire des simulations probabilistes du modèle avec une liberté complète dans le choix des variables d’entrée et sortie. Les variables connues (de manière certaine ou seulement en probabilité) sont entrées dans le réseau en tant qu’évidences. Des requêtes sont alors effectuées pour connaitre en probabilité les valeurs d’autre variables dans le réseau :

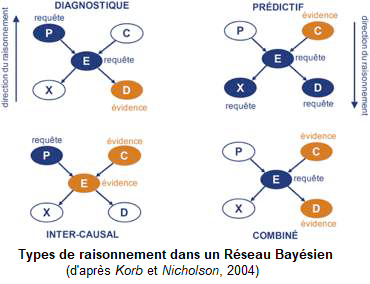
• Le raisonnement peut être diagnostique, pour inférer en probabilité la valeur des causes d’un effet observé
• Il peut être prédictif, pour déduire les conséquences d’un événement
• Il peut être inter-causal en utilisant la connaissance d’un effet et d’une de ses causes pour inférer la valeur d’autres causes possibles
• Il peut finalement combiner la connaissance (certaine ou floue) de tout sous-ensemble de variables pour effectuer une inférence probabiliste sur les autres.

Les réseaux bayésiens s’appuient sur le théorème de Bayes qui lorsqu’un événement A s’est produit, permet de déterminer quelle est la probabilité que la cause M_i l’ait produit ?

P(M_i | A) = P(A | M_i) x P (M_i ) / P(A)

  où    • P(M_i | A) : probabilité a posteriori
         • P(A) : constante (pour chaque M_i )

 ♦ Équivalent étranger : Bayesian network.